
We can say that the markets for gold, silver and Bitcoin are getting more and more positive. One of the sources we can rely on for this is the Trade Weighted Dollar Index.
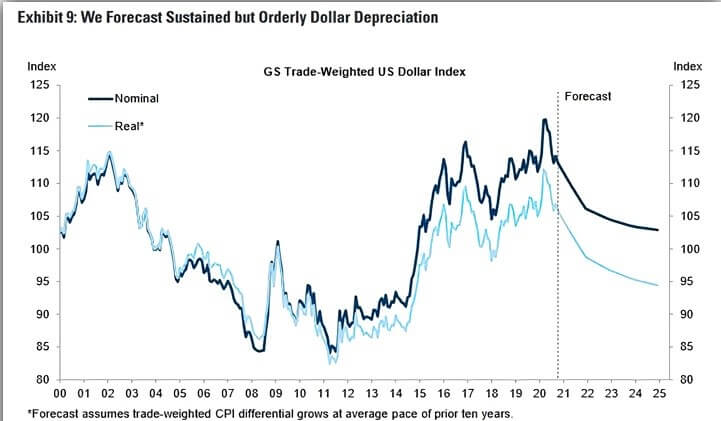
Source: Bloomberg, Goldman Sachs Global Investment Research
TWDI, which showed a rapid rise in the first months of 2020, has been in a regular downward trend since then. As seen in the graph, the downward trend will continue in the 5-year forecast made as of 2021. In the aforementioned forecast, it seems that the index will fall below the 95 level in real terms.
The difference between the trade-weighted dollar index, TWDI, and DXY is briefly this: While DXY is only found with the US dollar exchange rate of a few developed countries, TWDI is an index based on the trade volume made in dollars all over the world.
In fact, it is an index that gives more accurate results. In fact, as can be seen, it has been in a continuous decline since March 16, 2020. Of course, one of the factors that play an important role in the weakening of this index is that the FED is printing money to weaken the dollar.
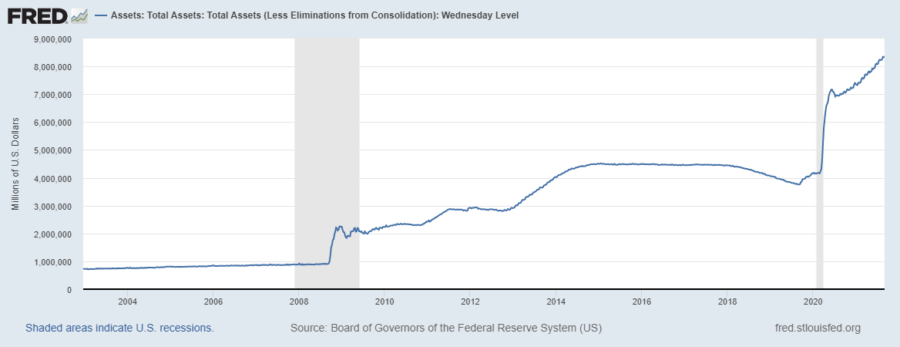
Source: https://fred.stlouisfed.org/series/WALCL
As can be seen in the chart, while the FED has printed approximately 3.7 Trillion Dollars since August 2019 until that period, it has printed approximately 3 times that amount, ie 8.4 Trillion Dollars, since then.
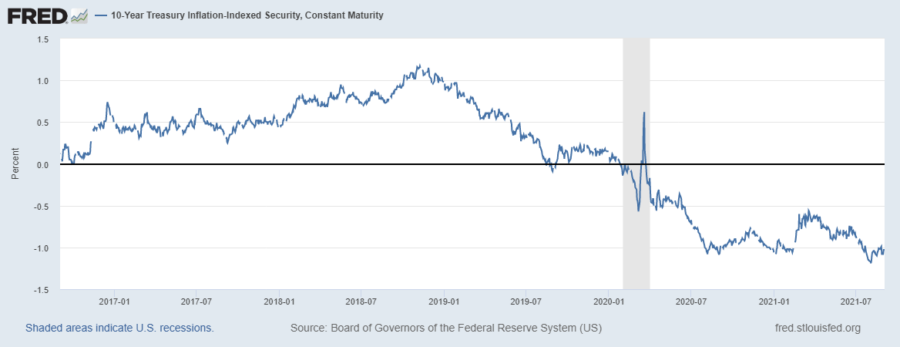
Source: https://fred.stlouisfed.org/series/DFII10
More importantly, the US 10-Year Treasury Inflation-Indexed Security rates are falling. It is the decrease in these interest rates that started the gold movement at the end of 2018. The reason for the slowdown in the increase in gold and silver prices in September-October 2020 is that these phases started to rise again.
As can be seen in the chart, these interest rates again trended downwards. There is no other way out. In this way, gold and silver prices led upwards again, albeit slowly. The reason why these interest rates started to fall was due to lower inflation expectations. However, this did not happen, and for the first time, inflation expectations began to be estimated above the level before the pandemic process. Why are gold and silver prices soaring as the price drops? Because, as the reserve currency, the dollar is not with itself, but with debt securities and the interests on them. In other words, when these interest rates fall in real terms, other tools used as value accumulation in the world come into play.
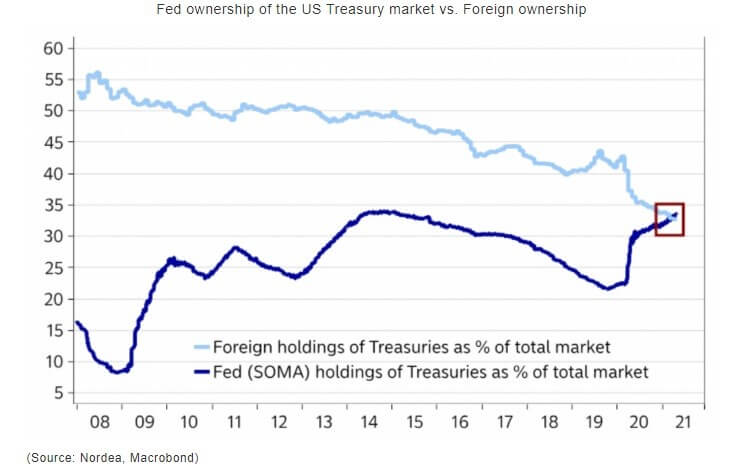
So primarily gold, silver and bitcoin. In other words, monetary assets produced on a limited basis. In 2008, foreign central banks, foreign companies, etc. We see that the interest of foreigners in these bonds has decreased, while the FED has increased their purchases of these bonds. Starting from 2008, FED embarked on an unprecedented dollar printing operation in American history. America, which minted less than 1 trillion dollars until 2008, has printed 6 times more money than it has printed in 200 years in approximately 12 years since that date.
This caused a kind of panic in other big actors of the world. They all started to sell these bonds. As seen in the chart, for the first time, the amount of bonds bought by the FED exceeded the amount of bonds bought by foreigners. While the American budget has an average deficit of 1 trillion dollars every year, the deficit increased to 3 trillion dollars during and after the pandemic. It prints money to cover these gaps. That’s why it issues these government bonds. Therefore, while the purchase of US bonds by the FED is increasing, it is not possible for the interest rates to go up in order to close this gap.
Finally, in this case, the positive mood towards gold, silver and bitcoin does not seem to change much.